In earlier articles the author suggested to extend the wave particle duality of physics to a triple, adding whirls. Whirls are mathematically computed differently than waves. Particles can be considered as a kind of bubble formation in other aggregate phase state. Wave equations have a

1-dimensional space expansion in direction where a wave is travelling. Harmonic waves for a vibrating string miss this coordinate. Sound expands through pressure on the other hand in a sound cone. Measured is its power as intensity per area (figure 1).

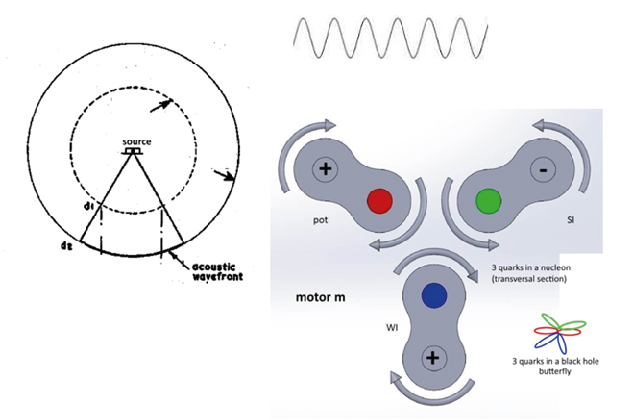
Figure 1.  At Left Accoustic Sound Whirl,   at Right Sinus wave, below a  Quarks Nucleon Bubble for  a Proton having 3 Quarks inside  a Solid Ball, Satisfying the Pauli  Principle; Waves or Whirls have  the Superposition Principle and come  in Wave or Whirl Packages  for Nucleons with 3 Quarks the Theory is decscribed in [1] ,  [13, video]

This suggests that conic whirls are an alternative for energy duality: making atomic or leptonic particle bubbles or moving linear in space like photons waves. Whirls can be used for quasiparticles and Gleason frame GF triples (like spin coordinates) are suitable for their quantum measures. One such GF triple shall be for the choice, energy makes in an experiment: in one experiment it shows wave, in another particle (photons for instance – the wave-particle duality), in a third whirl character (rgb-gravitons of MINT-Wigris for instance).

In the MINT-Wigris project (see researchgate.net) it is assumed that wave like quasiparticles come from decaying dark energy and that decaying dark matter like Higgs bosons release quarks and generate as decay products the bubbles of the two fermionic series.

For dark energy and matter are suggested  a pinched and a Horn torus with a singularity. Below are two models for this: dark energy has inverted frequency helix lines inside and their cylindrical location is closed at projective infinity by a double Minkowski cone. They have higher speeds than light inside the pinched  torus. In figure 1 is shown that quarks are inverted at the Schwarzschild radius to 1-dimensional lemniscates, drawn with two red or green or blue wings. All quarks are joined in this kind of pinched torus at their center as the Horn torus singularity. (figure 2) They are set free carrying one of the three olor charges r, g, b,in nucleons, but confined in nucleons by the two color charged gluon quasiparticles (field quantums) as an energy exchange. Gluons are whirls, often drawn as stretchable springs between two quarks as end points; different geometries are used in physics; MINT-Wigris attributes to them a vectorial conic rotation; rgb-graviton whirls are the neutral color charge of nucleons. In figure 1 is mentioned also a driving POT potential motor and a plasma flow since the observations are for high-speed flows in nucleons with a mixture of differrent energies as particles or quasiparticles. POT sets with a Higgs field the protons mass which is not additive the mass of 3 quarks (10 percent only), but the Einstein transition and interacting energies add 90 percent to the nucleon mass.  Is this also true for astronomic galaxies having possibly dark whirls, energies, matter?

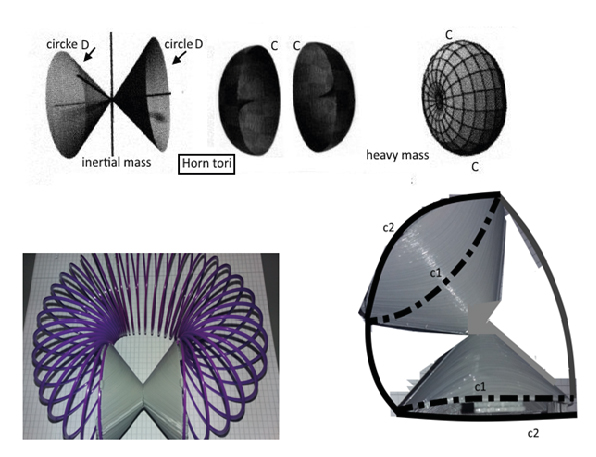
Figure 2. Double Cone, Two Hemispheres, Dark Matter Horn torus, below: Dark Energy Pinched Torus right: dark whirl; the boundaries black-dotted black are identified to one circle c form c1, c2

For dark whirls the dark energy Minkowski pinched torus can be replaced by closing the double Minkowski cone at projective infinity by a circle, deleting the cylindrical spring (helix line on a cylinder). This cone dark whirl has then to be extended; the diametrical cross cut is in space not

1-dimensional but a 2-dimensional sound wave front, maybe 3-dimensional as the astonomy noise from a big bang. This is neither bubbling nor dark energy since it is a conic front level, an area or surface on which this kind of energy expands like a decreasing potential on the surfaces with b/r, r radius, b a constant. The sound pressure level is Lp = ln(p/po) measured in N per meter² (p pressure, po a unit measure).The amplitudes of the whirls are decreasing.

Some research ideas: Sound wave fronts are observed in our environment as inverted dark whirls. For sound is known that it can be broken, for instance when the source as airplane gets another proportion towards the medium air. There is a number for this which maybe not that of inverting sound whirls energy from dark whirls. For a sound particle is listed in dictionaries: it is an imaginary infinitesimal volume of a medium that shares the movement of the medium in response to the presence of sound at a specified point or in a specified region. For the pressure on a volumes surface or an area the energy transfer uses also momentum and whirl motions can add friction. Phonons are for heat transfer energy and momentum, but they are not sound. Whirls have different shapes for their expansion in time. Mostly a rotation about the cone axis is added. Speed increases inside the cones when the motion is in direction of the cones tip. In a vector description, the initial point of the vector is kept fixed, the vectore traces out the cone surface and the endpoint of the vector describes the bounding circle of the cone. The different kinds of speed and geometries can come from a source in motion, compared with a mediums speed, from a source at rest as a vectorial rotation or from a spiralic acceleration towards a pinched point as tip of a conic whirl. Quasiparticles and waves expansion have also different kinds, speed orbits; they transfer (like phonons) energy and momentum between bubbles and act as exchange quantums. In physics the geometry of spin up/down is put on a nonorientable Moebius strip: if as vector normal or transversal rotated by 360 degrees it shows the opposite direction.The parity operator of physics identifies on a bounding 2-dimensional Riemannian sphere S² as oriented surface in space dianetrrical opposite points for a projective 2-dimensional space. This should be taken as space for quasiparticles. Graviational orbits of planets about a central sun join in to this ideas.  Take an additional Einstein plane E to spacetime with coordinates (x,y,z,ct), xyz-space, speed of light c scaled time ct, as complex cross product (xyz has the real cross product of Pauli spin SU(2) matrices) z₃ = (z+ict)x(x+iy) , written with complex quaternionic spacetime coordinates. Extend E to a projective plane by adding a projective line U(1), a loop or 1-dimensional circle at infinity. In E is then the planets P orbit C and E cuts a Minkowski Kepler cone such that the two cosmic speeds apply to C: Kepler computes the free fall case for a comet hitting earth, also the escape case (parabola or hyperbola projective quadric) for its or a planets escape from a central huge mass Q like a sun or a black hole or dark matter. Einstein adds through general relativity a phase angle when rotation occurs on a Kepler ellipse such that the ellipses main axis rotates between two concentric circles about the common barycenter of the system (rosette motion). The complex coordinates of E are z₃ = (f,w) where w can measure with a GF mass m as a nonnegative real scalar and f is an inverted time interval 1/∆t which can also be angular as ω = 2πf for whirls. Rescaling mass as mentioned for nucleons above is done by such a GF triple. The projective coordinates are [f,w e₈] and e₈ is a vectorial linear coordinate. MINT-Wigris has then for the strong SI interactions 8 SU(3) dimensions 7 octonian coordinates:

(e_{1,2,3,4,5,6,,8} ) = (x,y,z,w,f,U(1)-{∞}). The SU(3) Gell-Mann matrices λj, j = 1,2,3  are for the rgb-graviton and project the S³ sphere of the strong interaction down to the weak WI interaction Hopf SU(2) sphere S³.  SI has a toroidal trivial bundle geometry S³xS⁵  with a 5-dimensional sphere added. Hopf has for WI a nontrivial fiber bundle with the toroidal Hopf map h: S³→ S².  The S⁵  is tha space for a deuteron and atomic kernels bubbles complex projection g: S⁵ → R⁴ U S²  = CP², a complex inner spacetime for them with a bounding S² sphere. This space is provided by an inner differentiating-integrating dynamics and MINT-Wigris sets differentiating on the Heisenberg uncertainties on the space axes x,y,z with position at +x, mass for momentum (as d/dx) at -x, angle φ at +y,   dφ or  ω = dφ/dt at -y for rotation and angular momentum,  time collinear with +z and frequency as  e₆  coordinate at -z. Functions of radius are similar treated  with d/dr on x; spherical angles Θ are measured as usual towards the z-axis. This is not the missing 8th ocotninan coordinate discussed later on. A polar complex angle φ gives polar coordinates for the plane x + iy  = r∙exp(iφ)  and WI sets orientations for spacetime.  The projective P² can be a subspace of spacetime R⁴ It is gravity generated.  Gravity acts in CP² through the rgb-gravitons. In getting a chemistry deuteron sceletton for nucleons, the MINT-Wigris Tool bag has several models which can be stickked together from different parts in a bag. Essential is the tetrahedron with the rgb-graviton having the CP² center as tip and the two nuceleon base triangles at (+x,+y,-z), (-x,-y,+z) for a proton and a neutron. A differentiating WI isospin exchange between a paired ud-diquark generates a local deuteron space axis, either x or y or z. They are actually halfrays which can be split at the deuteron barycenter for the two nucleons in atomic kernels AK. The AK are build from such dinucleons kept together by a quasiparticle exciton. Integrating is with SI and a SI rotor in CP². There are videos to demonstrate them and also solid models for making the dynamical, discrete turns and not described here. Integration is for the energy exchange of the deuteron or AK with its environment and uses 6 polar hedgehog caps about the endpoints of the local axes.  6 energy vectors are set by the missing 8th octonian (units setting) coordinate e_o. +x has  electrical potential as energy or (differentiated) force vector attached and as measuring unit A ampere, -x has a mass force and integrated gravity potential and as measuring unit kg, heat at +y is measured by Kelvin, rotational energy and angular momentum is at y and has a derived measure, time imeasured in seconds s at +z with magnetic energy  measured in Volt, frequency and kinetic energy is measured in inverse seconds  and as

integrated or differentiated momentum attached to most energy carriers in the universe for its world line in free motion.  

It is necessary to introduce for all this the symmetry of Moebius transformations of S². A discrete tetrahedral  symmetry is the start. It factors through its normal subgroup of the id plus CPT operators Z₂ x Z₂ inro the triangle symmetry group D₃, the nucleon. Its members are the complex cross ratios as invariants under the Moebius transformations. This is in the sense of the Noether theorem: a geometry, invariants and symmetries belong together. The standard model of physics was construced this way:  WI has the S³ Hopf geometry and 3 generating Pauli matrices for the basic 8 quaternions and 3 weak bosons as exchange field quantums, SI has the S³ x S⁵ geometry and 8 gluons as field quantums, the electromagnetic interaction EMI has the loop U(1) symmetry, cylindrical coordinates for its helix frequency expansion in time and the exp exponential functions for wave descritpions. Observable ar real projections like cosine or sinus functions which can be local vibrations, harmonic or travelling cylindrical waves. As suggested earlier, POT as potential force has also projective geometries like P². POT is according to Schmutzer [12] a projective real, linear 5-dimensional spaace which unifies electrical EM with gravity GR fields. His projector sends it down to three 4-dimensional fields: EM, GR and neutral which may be neutral, empty spacetime without energy attached. Fields for instance for Higgs and its bosons have for POT radial equipotential and field lines in empty space, also flows or plasma driving around obstacles have sometimes such geometries. Complex evaluations through differential or integral equations are in use. Poles are like obstacles in the macroscopic world. Forces are like second derivatives 1/r² or d²/dt², potetnials or speeds like first derivates 1/r, d/dx or d/dt. Integrations are also for areas and volumes. Observe that potentials integrated have the multivalued complex log function, the inverse of exp. In the Tooö bag the 6-roll mill demonstrates such a plasma flow, as also suggested in figure 1 for a nucleon plasma flow. Computations with more complicated flows are available and described in catastoprhe theory [14]. The 6-roll mill and other gravity oriented tools have been constructed by this group of researchers. For the 6-roll mill the ellipitc catastrophe is suggested. Singular points or poles are replaced by higher degenerating geometrical objects, cusps for instance. The potential for the elliptic umbilic is described in detail.

Some figures are useful. Waves have not logarithm but the exponential function as the log inverse function for their description. The complex logarithm is multivalued by adding integer multiples of  arguments.  The logarthmic function is made single valued by drawing for every argument a complex plane and join them suitably at the negative horizontal line. (Figure 3)

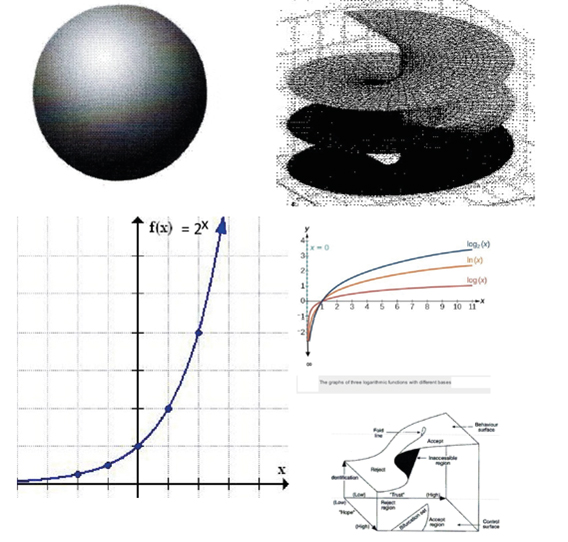
Figure 3. Bubble, Log Surfaces, below its Function, at Left  below an Exponential Function, below Cusp for Wrinkltons as Quasiparticles

On the other side the electromagnetic interaction waves EMI  show in experiments particle character. This is due to quantizations like E = h for their energy. EMI can show up not as wave which allow superpositions but as stochastically counted quanta as their energy quantums. If their wave function is used for the different geometries, the particles can be taken as one winding for the periodic wave functions energy when its in time expanding frequency travels along a helix line on a cylinder. The wave particles are finite cylinders, not a bubble as for other energy particles and the energy is only present in motion. These are not the strings of string theory which are interval oscillations like a harmonic wave with ends kept fixed. Excitations of this kind are not in the list of quasiparticles, photons are.

For matter sometimes solutions of differential equations can be give in form of matter waves. In this case the quantization means that the equations allow only discrete solutions because of the spin/orbital length quantization for particles where only mutliples of h/4π, h the Planck constant, are allowed. The example for this wave-particle duality are Schroedinger waves for electrons in an atoms shell. Their particles orbital wave length has to fit the radius of the orbit. EMI waves generated or absorbed can adjust this by changing the frequency of the particles motion. These two kinds of wave particle duality have in common quantized forms of EMI energy carriers. Photons for :this are only one kind of quasiparticles or excitations.

Looking at phonons as quasiparticles they act not this way, but can act for vibrations in crystals, or showing a stochastical expansion of heat. Solitons which can transport pressure are neither generating a wave-particle duality. Used for sound, amplitudes of harmonic waves together with oscillating strings ot string theory their diexcitation are generating sound waves. This is not a frequency quanta of EMI or an orbital frequency quanta of an electron related to its wave length. Take a vibrating string with a harmonic wave function when the string is set in motion. The ends of the string are kept fixed. Changing length as a violinst does means that the amplitude of the oscillation changes. The quanta for the strings length and pressure on the string (set in motion through strings) are responsible for the amplitudes (generted by solitons) of the generated harmonic wave. Sound expansion is conic, not like EMI. 

There are then (possibly) four kinds of energy characters and their carriers, waves, for the particle character decay products of Higgs bosons or dark energy like fermions and leptons, decay quasiparticles of dark energy which can be seen as having a whirl character (no wave equation) and these not clearly defined sound particles for a postulated sound Horn torus in figure 3 and the 3-dimensional big bang sound in astronomy. The string excitation is for harmonic oscillations inside the sound Horn torus, the solitons change their amplitudes.

The functional descriptions is for waves by the exponential function , for sound (possibly) the logarithmic function and its derivatives; for particles are useful matter waves and  the dihedrals polynomial equation zⁿ-1 with the nth roots of unity as solutions. The figure for this is a dihedral compass having n points on the bounding circle of the disc in equal angular distance. The compass needle can only change between the angular quantized units of the nth roots. The symmetry of order 2n has a rotation of order n and n reflections. In linear form for a vibrating string as a cosine projection for an exponential function the nth roots of unity count the number of a full periodic exponential revolution, for a cosine wave function from 0 to 2π. For particles the dihedral compass is used in the MINT-Wigris theory for the scaled general relativistic G-compass where the matrix G is of order 6 and  the turning of the needle sets on the segments between two adjacent roots a QCD color charge. They are not point charges like barycentrical mass. If the segments sides are identified, they can carry a vector of suitable length and the vector is set in rotation clockwise cw for one color charge and counterclockwise mpo for tis dual. The basic color charges are red, magenta, blue (turning cw), turquoise, green,yellow (turning mpo). These kind of quasiparticles is not in the offcial list. A magnon can be taken as quasiparticle for magnetism and its field quantum whirls. Quasiparticles have always their momentum, parallel or antiparallel to spin (in case they have one, - phonons or Higgs bosons have zero (no) spin). This kind of divectors occurs also as the helicity of neutral leptons and the divectors spin plus magnetic momentum replaces helicity for elecrical charged leptons.No quasiparticle is listed, but an exciton for electrons Cooper pairs shows that a vectorial v-exciton has to be added as quasiparticle or excitation. The first character is fermionic, the second case bosonic having a circular shape for a periodic function. Maybe neutrinos are 3-dimensional blow ups fromthe v-exciton vector and its Cooper circle for the spin rotation cw or mpo. The blow up shape has a spindle torus as 2-dimensional surface while an electron in the MINT-Wigris theory ahs a 2-dimensional Hopf sphere S² as shape. When this is 3-dimensional Hopf blown up, the Cooper circle on S² for the point charge of the electron is becoming a torus surface nd the charge islocated on a 1-dimensional leaning circle on the torus. Point charges blown up can this way have a 1-dimensional circle as geometical location. A color charge location is 2-dimensional. Blowing up a mass charge as point set by a Higgs field at a barycenter, it is possible to set mass on a Schwarzschild radius Rs. Since this is used for second escape cosmic speeds  v2²/c² used for orbiting systems about a central system, Rs is postulated as a 1-dimensional circle. This fits also the Hopf fiber bundle geometry  for electromegnetism with the SU(2) symmetry. A quasiparticle e-exciton sets circles and in the new version for blow ups it changes scalar point charges to a location on a circle.

This kind of changing dimension is projective. A projective 2-dimensional plane has as transformations correlations which also set quadrics. In the above case the correlation of a point [x,y,w] in projective coordinates has associated a line ax + by + cw = 0, a,b,c real constants. The quadric is setting the constants equal to the point corodinates in x² +  y² + w² = 0. The projective norming of w = 1 sets the unit circle x² + y² = 1. It presents fibers in the SU(2) geometry of S³, Hopf mapped down to S².  The same fiber blow up is assumed for deuteron and the strong interaction SU(3).  This has, as mentioned earlier, a 5-dimensional unit sphere S⁵ as factor and a fiber bundle with base CP². The deuteron has an inner spacetime inside the complex CP² bounding sphere S² and point color charges of 6 quarks in a deuteron atomic kernel are fiber blown up to circles in S⁵. In the above version of a color charge G-compass the circle charge was again blown up and sits on the cones surface. Dimensional blow ups of this kind are projective from 0 to 2 or 1 to 2 in a projective real P³ or P⁴ (complex CP²) space. The conic quadric is x² + y² – z² = 0. It can also be written with time replacing z and radius r replacing xyz-coordinates r² – c²t² = 0, c speed of light. These are two lines on a cones transversal section which can be rotated about the t-axis for getting the cone or a double Minkowski cone. The bounding circle from before can be dimensional extended to any  space dimension of radius. In dimension 1 the two lines are closed at infinity for setting a 1-dimensional lemniscate of quarks energy location inside a dark matter bubble. Their 3-dimensional blow up has a brezel of genus 2 as surface. Electrons Hopf leaning charge circle sits on a torus of genus 1 which is rotating about its central axis. A quasiparticle cr-exciton can set the circle for fibers in fiber bundles. For the exciton  coupling of two vectors like spin plus momentum it can set the blow up  their rotational particle form, for instance to neutrinos spindle torus surface. In physics mostly a Hopf sphere S² is drawn for neutrinos and the neutral charge rotates in cw or mpo direction on a latitude circle. Since spin has to rotate about a central rotation axis, the motion of neutrinos in space has the geometry of a coning spin rotation on the north pole of a S² sphere which moves on its world line in the momentum direction. In the case of electrons spin plus magnetic momentum (antiparallel to spin as in the neutrinos case for momentum) rotates about the torus axis. The momentum is not involved.  (Figure 4)   

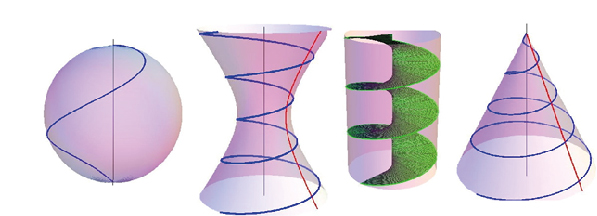
Figure 4. 3Dspirals

Quasiparticles occur in a rich variety of geometrical, local shapes in which they transfer energy and momentum towards the medium in which they move that mostly no direct functional description or symmetry can be associated with them. Above as geometry for them a projective plane is suggested since they have spin like vectors in up and down direction which use for the change a Moebius strip. The geometry for sound is the above described expansion in a Minkowski cone with equipotential sound front surfaces and flow/stream lines for pressure.

What can be taken as symmetry for pressure and sound? The quaternion Pauli generators for SU(2) are also available for the dihedral D4 as symmtery of order 8. SU(2) is itself not needed for sound. If the flat D4 is drawn 3-dimensional, a tetrahedron with 4 vertices is obtained. It is possible to take its symmtery S4 of permutating 4 letters or numbers a,b,c,d or 1,2,3,4. There is a normal subgroup of S4, the Klein 4-group Z2xZ2 which has the matrices id, -id and the third (with its negative as fourth Klein matrix) has rows (0,1), (-1,0). They present the P, C, T parity, conjugation, time reversal operators of physis and can be taken as a kind of S4 invariants for sound. Also the SU(2) quaternions have these subgroups in form of +id, -id, σ_{j ,} -σ_j.The projective spaces can be generated by projective duality or real (or complex) cross products in  a linear real space of dimension (n+1) in the form w(n+1) = w1xw2x...xwn. In case n =  2 the w(3) vector measures with its length the area spanned by the w1, w2 vectors, in case n = 3  a volume. Setting cross products  is from n = 2 on, but is not available for n =1. For this case a unit vector setting quasiparticle is assumed as a first e_o coordinate of an octonian space. This space the 4 dimensions of spacetime doubled up for an frequency e6 a mass e₅, a Kaluza-Klein e7 coordinate and e_o. A projective 4 to 4 duality appears in 9 projective dimensions where a point has an 8-dimensional dual and a 4 points generated space has a 4 dimensional space as dual. ) dimensions are one more than the SU(3) symmetry with an S³xS⁵ trivial fiber bundle. The Gell-Mann SU(3) matrices λj are listed as blow ups of the 3 Pauli matrices. But the blown up three σ₃ matrices ar linear dependent which makes the λj space 8-dimensional. Its λ₈ matrix can be split for the 9 dimensions needed into two diagonal matrices [1,0,-1], [0,1,-1] with λ₃ as [1,-1,0] as third σ3 blow up. The λj blow up adds a row and column of 0 coordinates to the Pauli matrices. To the Hopf/Pauli geometry as S³ as trivial fiber is added as space factor S⁵ to obtain S³xS⁵. For these unit spheres Sⁿ projective correlations can be used. The correlation between a point and a correlation quadric for a circle was in a P². The S² for a points dual quadric is in P³, for S³ use a P⁴ and for S⁵ a Pⁿ, n = 6. In case the SU(3) 3x3-matrices are replaced by 8 octonian coordinates (having another multiplication table) the e₁,…,e₆ coordinates are for spacetime (e4 for time)  and the others are listed above. The linear e₈ coordinate is stereographic closed by a point at infinity ∞ to a circle. In case for these spaces settings are needed quasiparticles, the quasiparticle cr-exciton is renamed to cn-exciton, n =1, and for other n =2, 3, 5 to a point is associated a correlation quadric Sⁿ.  

Concerning whirl measures, in [7] chapter 3 Gleason operators N as positive, self-adjoint, bounded operators of trace class 1 are constructed from a frame functions f of a frame GF.  Gleason operators have a probability measure associated. They have a subspace called support where on this subspace the measure is 0. MINT-Wigris uses them for quantum measurements. Choose for the P, C, T operators a suitable N operator. Then the sound measures can be obtained through GF quadrics f(x,y,z) = ax² + by² + cz² where x,y,z are frame coordinate for points pεS². The coordinates can be extended to complex or quternionic numbers. The constants of N can be  units a=1=b=c for pressure N/m² (N Newton, m meter), sound wave length m (v = λf as speed) and frequency f (Hz). The geometry S² is for a sound wave front. Other GF triple constants are chosen as (a,b,c) = (1/14,1/7,2/7) (proportions of basic spin length) or (1/6,1/3,1/2) (from electrical charge proportions) or (¼, ¼,1/2) (from the nucleons triangle with 2π/3 or  4π/3 rotations). The geometry of S² is obtained by the SU(2) Hopf projection of S³ to S² (middle case), from the SU(3) geometry CP² as boundary of a complex projective space for deuteron and nucleons (last case) and from basic spin lengths of rgb-graviton whirls in the first case. Matrix presentations for the GF vectors are sometimes available: The Klein group has as symmetry matrices of the dihedral D2 a rotation for P and two reflections C,T, as matrices can be taken for x,y,z of f(x,y,z) the Klein C,P,T matrices. For the electrical charge proportions the electrical charge f(x,y,z) quadric has for x,y,z three rotation matrices associated with rotations by πk/3, k = 1,2,3 of charge normed values. For the QCD quark triangle (in addition to the above rotation group members of its D3 symmetry) the first triple has color charge whirls which can have red on x (spin 1/2), green on y  (spin 1) and on z blue (spin 2). These are the rgb-graviton whirls three conic  whirls in superposition. If such GF‘s are available for other quasiparticle whirls, often the f(x,y,z) units are  1 and different  forces or coordinates are measured as above for N, also matrices can be associated. Spin has the three Pauli matrices on x,y,z and a=1=b=1 for equal spin length (m) of their coordinates. Heat transports with phonons (K Kelvin) energy (J Joule) and momentum (Ns) and a=1=b=c. For mass tiples GF the three numbers are mostly unequal in pairs a≠ b,c, b≠c. Magnetic flow quantums satisfy Φo = h/(2eo)  and have for its GF the units 1 for electrical charge (As measuring unit), h/2 for magnetic energy  ( Vs as measure) and for induction as an angular momentum with unit 1 (Nm/s as measure).

Magnetic field quantum whirls are stronger than the rgb-graviton and can make it decay. The green whirl is then a GF phonon (K measure) and it transports in matter/mass (density, measure kg/m³) energy as red whirl and momentum (Ns measure) as blue whirl. Density uses solitons as quasiparticles whirls and for electrons exist a lot of quasiparticles in different interactions with other systems. Rotations can have three unit vectors for a GF as spin (m), orbital momentum L (Nm/s) and their sum J = s + L with a=1=b, c=2. A GF for speeds (m/s)  can have linear speed with frequency f, angular speed with ω = 2πf and phase speed of sound with a=1=c and b = 2π.

For GF‘s the geometry is S². There are two 3-dimensional unit spheres S³h for the Hopf/Pauli weak and electromagnetic spacetime SU(2) geometry where the Hopf map blows down this sphere to h(S³) = S², a 2-dimensional sphere. The SU(3) geometry is S³xS⁵.  Take this sphere S³g for rgb-graviton whirls and its blow down of the Gell-Mann SU(3) 3x3-matrices λ1,2,3. Then all three basic forces gravity, weak, strong indicate that the S³ can serve for other kinds of energy transfer than only by quasiparticles. The Hopf/Pauli S³ from SU(2) is for the weak bosons as intermediate energy carrier which are generated from two colliding systems and decay acording to the Heegard decompositions and Feynman diagrams into two systems, exchanging their momentums direction. The rgb-graviton geometry S³ from SU(3) serves in nucleons for three color charged r or g or b quarks that they can exchange gluons energy  for their confinement in the nucleon, otherwise single quarks or diquarks  would decay. The confinement needs three color charges and also a SI rotor for the inner dynamics of nucleons. In a deuteron atomic kernel the forming of  ud diquarks which are on opposite coordinate locations x or y or z the quark decay is used for an isospin exchange between them; a u quark releases a weak W+ boson and the partner d-quark absorbs the W+ energy and becomes a u-quark; the partner u-quark becomes a d-quark. The local coordinates x or y or z are generated this way. The diquarks for the SI rotor are rb and gb. The third quark g or r is in the two cases used for setting in rotations three barycentrical coordinates of the nucleon which join this point with the barycenter on the rb or gb side of the triangle. These energy exchanges in a nucleon/proton and deuteron atomic kernel make them energetically stable inside a bubble for their particle character in space. They satisfy the Pauli principle: identical ones cannot occupy the same space location. Wave and also some whirls can have superpositions and come in wave or whirl packages. The dual character wave or particle for energy carriers showing up in some experiments is not the character-answer for three characters which include quasiparticles and whirls. Energy transfer between systems require a new view on this. For experiments is mentioned that in the quantum range the Copenhagen interpretation sets a nonclassical view: the measured system has to be prepared for the experment, after the experiment it can change its state. The measuring apparatus can have beside scalars as output, mutlivalued items in form of real numbers, but also in form of vectors (spin measure) or in matrix form. The matrices can occur with the ordinary multiplication, but also as spinor or tensor matrices. Physics may have some more outputs of experimental measurements.

MINT-Wigris has a flow chart to be followed: important are six energies, 4 forces, a lot of symmetries, physical systems, geometrical shapes, measures including new ones like the GF, new coordinate descriptions, also for functions. Fields and flows are rarely discussed until now. Maybe some experts on this join in and extend their theoretical view for MINT.-Wigris. (Flow Chart)

Flow Chart:

References

1. G. Kalmbach H.E (2017) Mint-Wigris, Mint Verlag, Bad Woerishofen. [crossref]
2. G. Kalmbach H.E (2019) with U. Eberspaecher, MINT-Wigris Tool Bag, Bad Woerishofen.
3. Dihedral. [crossref]
4. A. Beutelspacher et al. (1998) Projective Geometry. Cambridge Univ. Press, Cambridge UK. [crossref]
5. Seymour  MH (2010) Quantum ChromoDynamics. 97-143. [crossref]
6. Georgi H (2009) Weak interactions and modern particle theory. Dover Publ  Mineaola. [crossref]
7. G. Kalmbach  (1998) Quantum Measures and Spaces. Kluwer, Dordrecht. [crossref]
8. G. Kalmbach  (2019) Deutsche Nationalbibliothek Frankfurt/M. 1-39. [crossref]
9. G. Kalmbach H.E (2017) Deuteron States. Nessa J  Phys 1: 1-17. [crossref]
10. G. Kalmbach H.E (2018) Deuteron States Model. J Laser Opt Photonics 5.
11. Douglas N. Arnold (2014) Moebius Transformations Revealed. [crossref]
12. Schmutzer E (2004) Projektive einheitliche Feldtheorie. Harry Deutsch, Frankfurt. [crossref]
13. G. Kalmbach H.E (2019) Models for teaching the basic four interactions of physics.
14. Poston T, Stewart I (1978) Catastrophe theory and its applications. Pitman, London.  [crossref]